La Encuesta from Mgam
jueves, 8 de noviembre de 2012
martes, 16 de octubre de 2012
martes, 11 de septiembre de 2012
Ecuaciones Con Materiales
Ecuaciones Con Materiales
Matriz traspuesta.
Es la matriz que obtenemos de cambiar las filas por las columnas. La traspuesta de A la representamos por AT. Ejemplo :

Matriz adjunta Es la matriz que se obtiene al sustituir cada elemento por su adjunto.

Matriz inversa La matriz inversa de A es otra matriz que representamos por A -1 y que verifica:

Solamente tienen inversa las matrices cuadradas cuyo determinante es distinto de cero. Propiedades de la matriz inversa La inversa del producto de dos matrices es el producto de las inversas cambiando el orden.
Ejemplo: cálculo de la inversa de la matriz:

Para calcular la inversa, primero calculamos el determinante:

Después calculamos cada uno de los adjuntos :

Aplicación a la resolución de sistemas de ecuaciones lineales.

Aplicación a la resolución de ecuaciones matriciales.

martes, 4 de septiembre de 2012
jueves, 19 de julio de 2012
martes, 17 de julio de 2012
Ecuacion De 2º Grado
Ecuaciones de segundo grado y una incógnita
Sabemos que una ecuación es una relación matemática entre números y
letras. Normalmente se trabaja con ecuaciones en las que sólo hay una
letra, llamada incógnita, que suele ser la x.
Resolver la ecuación consiste en encontrar un valor (o varios) que,
al sustituirlo por la incógnita, haga que sea cierta la igualdad.
Ese valor es la solución de la ecuación.
Ejemplo: Resolver la ecuación x − 1 = 0
El número que hace que esa ecuación sea cierta es el 1, ya que 1 – 1 = 0, por lo tanto, 1 es la solución de la ecuación.
Si en la ecuación la incógnita está elevada al cuadrado, decimos que es una ecuación de segundo grado (llamadas también ecuaciones cuadráticas), que se caracterizan porque pueden tener dos soluciones (aunque también una sola, e incluso ninguna).
Cualquier ecuación de segundo grado o cuadrática se puede expresar de la siguiente forma:
ax2 + bx + c = 0
Donde a, b y c son unos parámetros que habrá que sustituir por los números reales que corresponda en cada caso particular.
y queda
x – 3 = 1 y x − 3 = −1
Si
x – 3 = 1
x = 1 + 3
x = 4
Si
x – 3 = −1
x = −1 + 3
x = 2
Por lo tanto x1 = 4 y x2 = 2
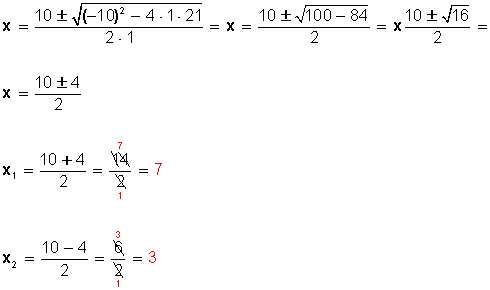
miércoles, 13 de junio de 2012
jueves, 24 de mayo de 2012
Fatorizaciòn de monomios y polinomios
Factorización
Factor
común monomio:
su formula es la siguiente:
Ejemplo:
Factor común polinomio:


Suscribirse a:
Comentarios (Atom)